NOTES:
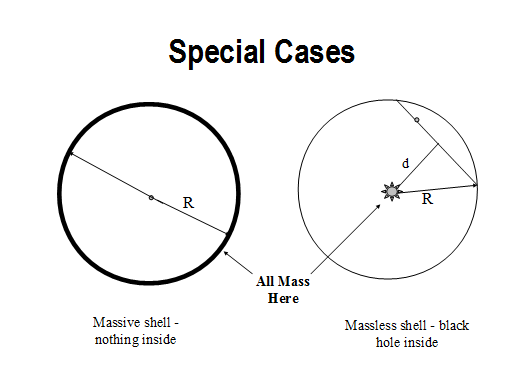
Deciding which mass distribution results in the quickest trip is a good test of intuition. For the black hole case, the object accelerates down a gravity well that gets very deep, but spends a great deal of time in the very flat part of the well. In the hollow shell case, all the acceleration happens during the trip through the shell and the rest of the trip is at a constant speed - the question is what that constant speed is. It turns out that the delta velocity due to the trip through the shell gets smaller as the shell gets thinner, so the total time to get across the shell can get arbitrarily long (the velocity gained during the trip through a thin shell is the square root of the acceleration of gravity at the surface of the shell times the thickness of the shell - but watch the units).
For the black hole case, the funny thing is that the longer the trip, the shorter the time it takes. For a very short trip, the roundtrip time is only slightly shorter than the 84 minutes we arrived at for the solid earth case, because even for the solid earth case, almost all the mass of the earth can be treated as if it were compressed at the earth's center. For longer trips (trips that go closer to the center to the earth), the object gains a lot of velocity by cutting close to the infinite gravity well - simulations indicate that by going within a couple of miles of the black hole, the length of the round trip declines to about an hour.
