NOTES
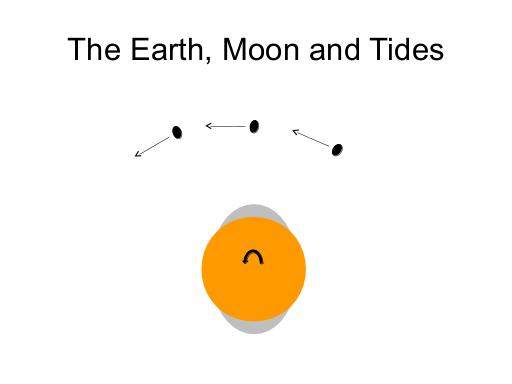
This is a picture of a planet with an ocean, and its orbiting moon. There are three possible positions for the moon relative to the tidal bulge - ahead of the bulge, directly above the bulge, or behind the bulge. Which description matches the Earth and its Moon?
This is a nice "gotcha" question. Although the Moon causes the tidal bulge, the bulge is "ahead" of the Moon - if you were watching the moon and tides, you'd see the tides at their maximum before the moon was overhead. Why? Because the Earth rotates faster than the Moon orbits, and because water takes time to move. As the Earth rotates, the pile of water that the Moon's tides created rotates with it; the bulge moves relative to the Earth's surface, towards the correct position under the moon, but can not move fast enough to get to that position. As the water moves in opposition to the Earth's rotation, it naturally slows the Earth, through friction; meanwhile, the bulge of water (and of the Earth itself) is pulling on the Moon, resulting in the Moon moving further from the Earth, and thus slowing down the Moon down as well.
You might think that the tidal forces should be symmetric - so that the amount that the Moon slows the Earth by pulling on the nearest lump of water would be exactly balanced by the amount that the moon is speeding up the Earth's rotation by pulling on the further lump of water, but that turns out not to be the case for the reasons illustrated on the next slide.
At the con someone asked me what the phase difference between the position of the moon and the position of the tidal bulge really is; I didn't know the answer, so I looked it up afterwards. According to this site http://www.lhup.edu/~dsimanek/scenario/tides.htm which I discovered after the convention (and which has a very nice discussion of all sorts of tidal issues), the phase difference is only 3 degrees, which is pretty small.
