NOTES
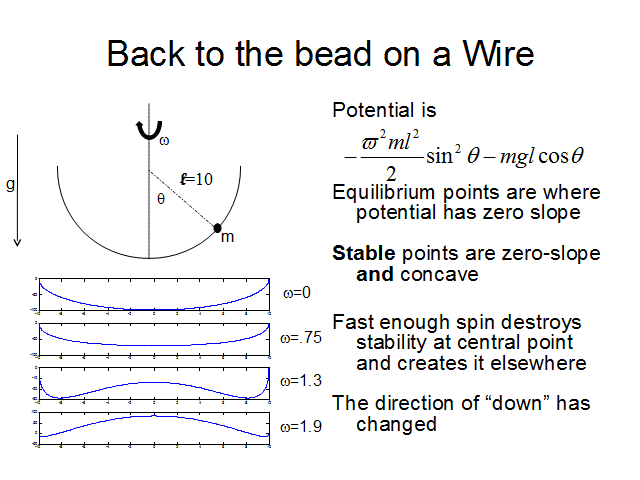
Because we can talk about forces, we can also talk about potentials, and calculate potential energy wells, which is really useful if you want to find equilibrium points and stable equilibrium points of a system, since equilibrium points are where the slope of the potential is zero, and stable equilibrium points are where the slope of the potential is zero and the potential curves upward (or in other words, is concave up).
I've shown the potential well for the non-spinning case, which looks just like the original semi-circle (except for the way I've scaled things), and for three different values of spin rate. At low spin rates, the bottom of the potential well becomes shallower, but still is concave at the bottom, but at a critical spin rate, the equilibrium point at the center stops being a stable point, and two new equilibrium points appear - both are stable points. As the spin rate increases further, the new stable points move further and further away from the center. The direction of "down" has changed because the combination of gravity and centrifugal force; in fact, if you took a non-spinning wire shaped like the potential well, the bead would move on that wire the same way that the bead moves on the spinning semicircular wire.
